L'ABONDANCE DANS TA MAISON

La difficulté donne prix aux choses.

L’Abondance et le Polynôme minimal d’Évaris Galois.

la somme des entiers positifs diviseurs.

Ils s'enivrent de l’ABONDANCE de ta maison.

 

Psaume 36

1	Au maître de chant. De David, serviteur de Yahweh.
2	L'iniquité parle au méchant dans le fond de son cceur; la crainte de Dieu n'est pas devant ses yeux.
3	Car il se flatte lui-même, sous le regard divin, doutant que Dieu découvre jamais son crime et le déteste.
4	Les paroles de sa bouche sont injustice et tromperie; il a cessé d'avoir l'intelligence, de faire le bien.
5	Il médite l'iniquité sur sa couche; il se tient sur une voie qui n'est pas bonne; il ne rejette pas le mal.
6	Yahweh, ta bonté atteint jusqu'aux cieux, ta fidélité jusqu'aux nues.
7	Ta justice est comme les montagnes de Dieu, tes jugements sont comme le vaste abime. Yahweh, tu gardes les hommes et les bêtes:
8	combien est précieuse ta bonté, ô Dieu! A l'ombre de tes ailes les fils de l'homme cherchent un refuge.
9	Ils s'enivrent de la graisse de ta maison et tu les abreuves au torrent de tes délices.
10	Car auprès de toi est la source de la vie, et dans ta lumière nous voyons la lumière.
11	Continue ta bonté à ceux qui te connaissent, et ta justice à ceux qui ont le coeur droit.
12	Que le pied de l'orgueilleux ne m'atteigne pas, et que la main des méchants ne me fasse pas fuir!
13	Les voilà tombés, ceux qui commettent l'iniquité! Ils sont renversés, et ils ne peuvent se relever. Une lumière extraordinaire «Une lumière extraordinaire brille au fond des ténèbres. C’est pour cette lumière que nous avons le courage de plonger dans l’obscurité. Pour y arracher du fond des abîmes notre perle divine.» Nombre abondant

En mathématiques, un nombre abondant est un nombre entier naturel non nul qui est strictement inférieur à la somme de ses diviseurs stricts ; autrement dit, c'est un entier n strictement positif tel que (en ajoutant n de part et d'autre de l'inégalité précédente) :

2n< σ(n),

où σ(n) est la somme des entiers positifs diviseurs de n, y compris n cette fois.

Les nombres abondants ont été introduits vers 130 de notre ère par Nicomaque de Gérase dans son Introduction à l'arithmétique.

Leurs premières valeurs sont : 12, 18, 20, 24, 30, 36, ... (voir suite A005101 de l'OEIS).

La valeur σ(n) – 2n est appelée abondance de n. Les nombres dont l'abondance est nulle sont les nombres parfaits, et les nombres dont l'abondance est strictement négative les nombres déficients.

Un nombre abondant dont l'abondance est égale à 1 est appelé quasi-parfait, mais on ne sait pas à l'heure actuelle s'il en existe. Par contre, on remarquera que 20 a une abondance égale à 2.

Tout multiple strict d'un nombre parfait ou abondant est abondant. Il existe donc une infinité de nombres abondants, à commencer par les multiples stricts de 6.

Abundant Number

An abundant number is a positive integer  for which

S(n) Ξ σ(n) – n >n,

(1)

where  σ(n) is the divisor function and  S(n) is the restricted divisor function. The quantity  σ(n) – 2n is sometimes called the abundance. The first few abundant numbers are 12, 18, 20, 24, 30, 36, ... (Sloane's A005101). Abundant numbers are sometimes called excessive numbers.

There are only 21 abundant numbers less than 100, and they are all even. The first odd abundant number is

945 = 3³.7.5

(2)

That 945 is abundant can be seen by computing

s(945) = 975>945.

(3)

Any multiple of a perfect number or an abundant number is also abundant. Every number greater than 20161 can be expressed as a sum of two abundant numbers.

Define the density function

A(x)Ξlim|{k<=n :σ(k)=>xk}|/n

(4)

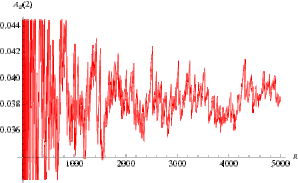
(correcting the expression in Finch 2003, p. 126) for a positive real number x where B gives the cardinal number of the set B, then Davenport (1933) proved that A(x) exists and is continuous for all x, and Erdős (1934) gave a simplified proof (Finch 2003). The special case A(2) then gives the asymptotic density of abundant numbers,

A(x)Ξlim # abundant numbers <= n /n

(5)

Wall (1971) and Wall et al. (1977) showed that

0,2441 < A(2) < 0.2909

(6)

and Deléglise (1998) showed that

0,2474 < A(2) < 0.2480

(7)

A number which is abundant but for which all its proper divisors are deficient is called a primitive abundant number.

 

CONSCIENCE

 

Selon le FERMATON (la plus petite unité de la conscience humaine) et la LOI D’ÉQUILIBRE D’EINSTEIN, abondance de n, s’exprime mathématiquement par une différence aussi par une auto nombre et d’un polynôme minimal de GALOIS selon l’équation suivante :

 x² +2x – β = 0

β : ƒ(Marqueur universel du FERMATON(la plus petite unité de la conscience humaine).

Dr. Clovis Simard, phD